Embedding - A Portal to Another Universe
- Oktay Sahinoglu

- Sep 11, 2020
- 3 min read
Updated: Mar 18, 2021

Embedding is actually a change of space. Thus it is basically a matrix multiplication. Embedding is generally used to take projections of higher dimensional vectors into a relatively low dimensional space. However it is not mandatory to think of just reducing the dimension. Somehow if you would like to increase your dimension, you are welcome too.
In Machine Learning area, Embedding is mostly used to define a large number of categorical variables more effectively (normally end up with huge one-hot encoded vectors), such as word vectors in NLP.
By using Embedding, we can;
Reduce computational complexity
Reduce storage complexity
Increase robustness
Increase interpretability
Enable visualization (2D and 3D cases)
Let's assume we have "N" features defined by vectors in "D" dimensional space. And we would like to move to a new space with "K" dimensions. The key to the portal between these two spaces is an "DxK" size Embedding Matrix.

What would be the values of the Embedding Matrix?
Of course it depends on your purpose of changing space. There are different types of methodologies for Embedding, e.g.;
Principal Component Analysis (PCA)
Linear Discrimination Analysis (LDA)
Machine Learning Embedding Layer
Word2Vec
Glove
fastText
CoVe
ELMo
BERT
GPT/GPT2/GPT3
Some of them are statistical computation based, some of them are machine learning based and more sophisticated.

Although machine learning based methodologies generate a model rather than a matrix, all of them end up trying to get the projection of the old space onto a new space. This actually comes to the point of determining or learning the values of the Embedding Matrix.
For instance, if the variance of the data is important to you and you want to project into a lower dimensional space with Principal Component Analysis (PCA), you will compute an Embedding (Projection) Matrix accordingly; or if class separation is important to you and you want to make a projection with Linear Discrimination Analysis (LDA), you will compute a different Embedding Matrix.
On the other hand, thanks to machine learning based methodologies, you can learn the values of Embedding Matrix instead of computing. The simplest way, you can directly add an Embedding layer to your Machine Learning model and learn the values of your Embedding Matrix in a nonlinear fashion according to the optimization of your problem. Here are some simple code (PyTroch and Keras) examples of an Embedding Layer in a model.
PyTorch sample
import torch
import torch.nn as nn
class MyModel(nn.Module):
def __init__(self, origin_dim, embedding_dim, hidden_dim, num_layers, num_of_features):
super(MyModel, self).__init__()
self.embedding = nn.Embedding(origin_dim, embedding_dim)
self.lstm = nn.LSTM(input_size=embedding_dim + num_of_features,
hidden_size=hidden_dim,
num_layers=num_layers,
batch_first=True,
bias=True,
dropout=0.2)
#
# continuation of your model
#
def forward(self, categories, feature_values, ...):
# Assuming your dataset is built for LSTM
embeds = self.embedding(categories)
# output is bs, ts, emb_dim
features_combined = torch.cat([embeds, feature_values], 2)
# output is bs, ts, emb_dim + num_of_features
lstm_out, _ = self.lstm(features_combined)
#
# continuation of forwarding
#
return loss, outputKeras sample
import keras
categories = keras.layers.Input(shape=(1,))
feature_values = keras.layers.Input(shape=(num_of_features,))
embedding_layer = keras.layers.Embedding(
input_dim=origin_dim,
output_dim=embedding_dim)(categories)
embedded_values = keras.layers.Flatten()(embedding_layer)
features_combined = keras.layers.concatenate([embedded_values, feature_values])
output = keras.layers.Dense(output_dim)(features_combined)
Deep learning frameworks like Keras, PyTorch or Tensorflow expect a scalar, for example a consecutive number for each categorical variable, as Embedding input. You can imagine that one-hot encoded version is being used at the backend.

Learning of Embedding Matrix
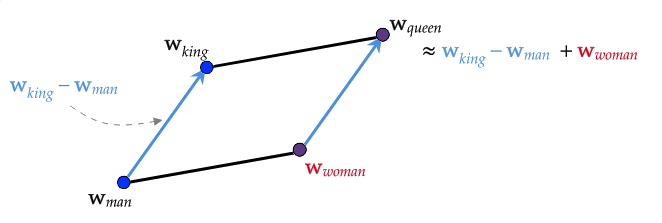
Moreover, methodologies like Glove, Word2Vec or fastText can provide you with more sophisticated Embedding Model, by which you can move to a new space where dimensions can contain the information on the relationships between features (or words) built in.
Furthermore; ELMo, BERT and GPT/GPT2/GPT3 kind of much more sophisticated models can provide a dynamic Embedding Model which gives you different results for the same input depending on the properties of the input, for example, positions and neighbors of words in a sentence. The input word "ring" can give you different output vectors for the sentences "My wedding ring is so beautiful" and "Boxers were ready in the ring". With these ultimate level models, besides the built-in information (such as relationships) defined by dimensions, some dimensions of the new space can hold different kind of information such as context.
As a summary;

Last but not least, you shouldn't think that you can use word embedding techniques for only words, you can use all these techniques for any categorical feature you want to move into a new space containing smarter information with less dimension. (Imagine the tokenIDs shown above as categorical features IDs)
Hope this helps! See you in another post.







Comments